The problem with Euler Angles
Everything has its place in software development. However, I have often found the ubiquity of Euler Angles in 3D applications to be a hindrance to programming complex systems that involve 3D orientation.
Their primary advantage is being the most intuitive of the mathematical representations of rotation we have. Nobody wants to input a matrix, axis-angle and especially not a scary 4-dimensional quaternion. And while Euler angles are useful for user input and some camera systems, in my experience everything else in computer graphics can be handled extremely efficiently and, to an extent, intuitively with quaternions.
To many developers, quaternions are black magic: you plug in some numbers, and you can rotate objects beautifully, smoothly, without mucking around with Euler angles. For my game 9.8, Euler angles are the worst because everything I do is in the player’s local space.
The Maths of Quaternions
While a mathematical understanding of quaternions will give you a deeper appreciation of maths and the clever people who make it, a deep knowledge is not required to use quaternions when you are using a game engine that implements them for you. The best explanations of the intuition I’ve found are from 3blue1brown , and 3D Math Primer for Graphics and Game Development .
Some basics are required though:
A quaternion is a 4-dimensional number that encodes a particular 3-dimensional orientation.
An important note: a delta rotation or ‘change in rotation’ is the same as an absolute rotation from the identity quaternion (FQuat::Identity), or no rotation. They just have different names: a ‘Rotation Quaternion’ and an ‘Orientation Quaternion’.
How to use Quaternions
Ignoring the 4-dimensional unintuitive bit, to make a quaternion (in UE4, an FQuat) you can:
Convert from a Rotator (Euler Angles)
Convert from a Matrix (will only convert rotation: Quaternions don’t do translation)
Convert from a rotation axis (a unit length
FVector) and a rotation angle (float)
The most efficient of these is the axis-angle approach, because under the hood quaternions use something similar.
I have found the easiest way to use quaternions in practice is like this:
- Find a vector that you would like to point in the direction of some other vector, such as the current player local z-axis and the opposite of the current gravity direction.
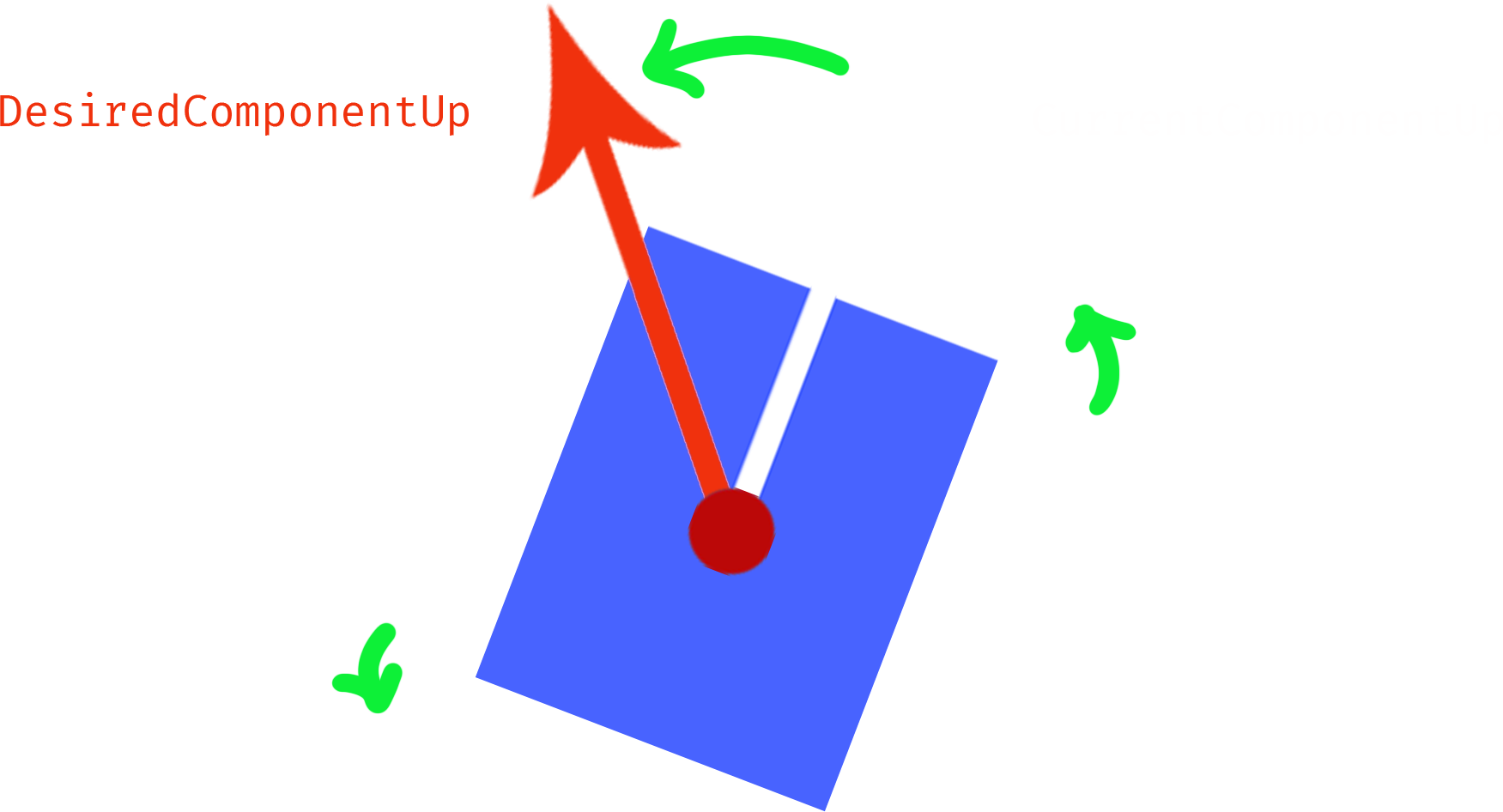
- Calculate the dot product of those two (unit) vectors, and then use the arccos function (
FMath::Acos()in UE4) to find the angle between the two vectors.
const float Angle = FMath::Acos(FVector::DotProduct(CurrentComponentUp, DesiredComponentUp));
For more info on dot products I refer you to 3blue1brown again, but all you need to know for this is:
as your two vectors are unit vectors, or vectors of size 1, this reduces to:
And using arccos (cos-1) to solve for the angle:
- To find the axis of rotation, we need a vector that is perpendicular to both vectors. Luckily, there is also an operation for that:
const FVector Axis = FVector::CrossProduct(CurrentComponentUp, DesiredComponentUp).GetSafeNormal();
The vector cross product will do exactly that. It needs to be normalised because the FQuat constructor expects that. You should also check the angle is positive1
before performing the cross product and normalising. If the angle is zero you can skip the actual rotation step as an optimisation.
- Now we can make the quaternion!
const FQuat DeltaRotation = FQuat(Axis, Angle);
- You’ve created a quaternion! It is completely fine if the level of maths required might mean this process is outside your comfort zome, that’s how learning works. Trust me, it’s worth it.
Now we can apply this to our actor with
AddRelativeRotation(DeltaRotation);
As you can see, using the AddRelativeRotation(...) function we avoid any scary quaternion multiplication. But you will probably need to use it at some point, so let’s dive deeper into how quaternions are used in UE4.
To rotate a vector, you don’t need to fiddle around with conjugates and inverses because UE4 has you covered: FQuat::RotateVector and FQuat::UnrotateVector abstracts all that away. Under the hood it does a clever optimisation
of the rotation (conjugate
) operation, where p is a quaternion with its complex part equal to the vector to rotate.
Ok, what about if you want to combine two rotations? Or find the difference? Or apply a rotation in local or world space? This is where it gets complicated. There’s not much to be done here except memorise or learn why this is the way it is.
Possible operations using Quaternion multiplication:
Apply a rotation in world space:
DeltaQuat * ActorQuat;
Apply rotation in local space:
ActorQuat * DeltaQuat;
You will notice that in quaternion multiplication, order matters. For C = A * B, first B is applied, then A (right first, then left).
Find the difference between two orientations:
NewQuat * OldQuat.Inverse();
Convert a quaternion from World to Local space:
ActorQuat.Inverse() * WorldQuat;
Convert a Quaternion from Local to World space2 :
ActorQuat * LocalQuat;
Even if you like FRotators, quaternions still come in handy. To convert a Rotator from local to world and vice versa it is often easiest to convert to quaternions and back using the above formulas.
QuatLocalToWorld(LocalRot.Quaternion(), ComponentQuat).Rotator();
and similar.
I created an implementation as a header-only static library , so you don’t need to remember.
I hope I have cleared up some questions surrounding quaternions and their use in UE4. You can choose to make them your formidable enemy or your powerful ally, it’s up to you.
Notes
Positive because the cos-1 () function is always positive or zero, never negative.
You will notice this is the same operation as applying a rotation in local space. This is due to the lack of distinction between a ‘Rotation Quaternion’ and an ‘Orientation Quaternion’, I’ve included it twice to make it clear what to do for seemingly different situations. The main point of the static library is to make it clear to people reading your rotation code what is going on without needing to decipher the multiplications and inverses.
Resources mentioned in this page:
- Quaternions:
- Dot products:
- Quaternion operation static library .